Desystemize #9

What do revolutionary new Sudoku techniques teach us about real-world problem solving?

On the heels of Representation and Uncertainty telling us to think more critically about our ontologies, I’d like to share a success story of ontological remodeling – that is, using new language to describe an existing thing. The existing thing in this case is the puzzle game Sudoku, which might seem a bit too straightforward to be described in a new way. You’re placing the digits 1 to 9 in a 9x9 grid without repeating a digit in a row, column, or box. There doesn’t seem to be space for unrepresented details in the way we’re interested in.

But here’s a quote from a January 2022 video of a man named Simon solving a Sudoku:

I now understand how to explain what’s going on in the puzzle. What I can tell you, what we’re going to end up with here, is that this digit, this digit, and this digit are a 1, 2, 3 triple. And isn’t it amazing? This, to me, is quite beautiful. I can tell you without fear of contradiction, if I had tried this puzzle two years ago…well, unless there is something else here that I’m not spotting, I might never have spotted that. Yet nowadays, because set equivalence theory has become so ingrained and practiced, it’s a very quick spot. And that being a 1, 2, 3 triple is just remarkably gorgeous. So how do we prove this is a 1, 2, 3 triple…? I mean, this puzzle could appear in the World Puzzle Championship now. There’s no way this could have appeared a few years ago, no one would have been able to do it! But now, that break-in is so well-signaled it’s almost fair!

We haven’t made any breaking new discoveries about the digits 1 to 9. But this set equivalence theory, whatever it is, has changed how Simon views puzzles so much that it’s not even comparable to two years ago. It’s all still just digits in a grid, but describing them differently leads you to a new conclusion. And precisely because Sudoku is so simply defined, the case study of set equivalence theory is worth studying. If we can find hidden secrets here, in a 9x9 grid of single digits, we can find them anywhere.

Let’s start by explicating the existing, “normal” ontology for a Sudoku. The rules specify that you have exactly one of each digit from one to nine in every row, column, and box – so it’s no surprise that these are the usual terms used to describe Sudoku puzzles. For example, you might say “I know that row 2 needs a 3, and it can only go in to this square,” or “Box 5 already has a 9, so the 9 can’t be in any of the other cells in box 5.” Because the explicit impact of the rules is based on these sorts of divisions, it’s a very useful ontology to have.

But that’s not the only way you could describe a Sudoku. You could partition the grid into an orange ostrich head and a fat green frog:

There are things you can say about these shapes. No digit can appear in the ostrich head more than three times, because its only in three boxes total. A digit that appears on one of the frog legs won’t appear on the other, because they’re in the same row. While these claims are true, they’re ultimately just pointing back to the words we were comfortable with already. Drawing the ostrich and the frog didn’t really accomplish anything.

Ontologies can’t exactly be wrong, since they’re just methods of description. But it’s pretty obvious that this one isn’t useful. It doesn’t let you state anything new that you couldn’t state using your previous vocabulary. It’s just an unnecessary level of abstraction that has to be peeled away to get to the useful ontology.

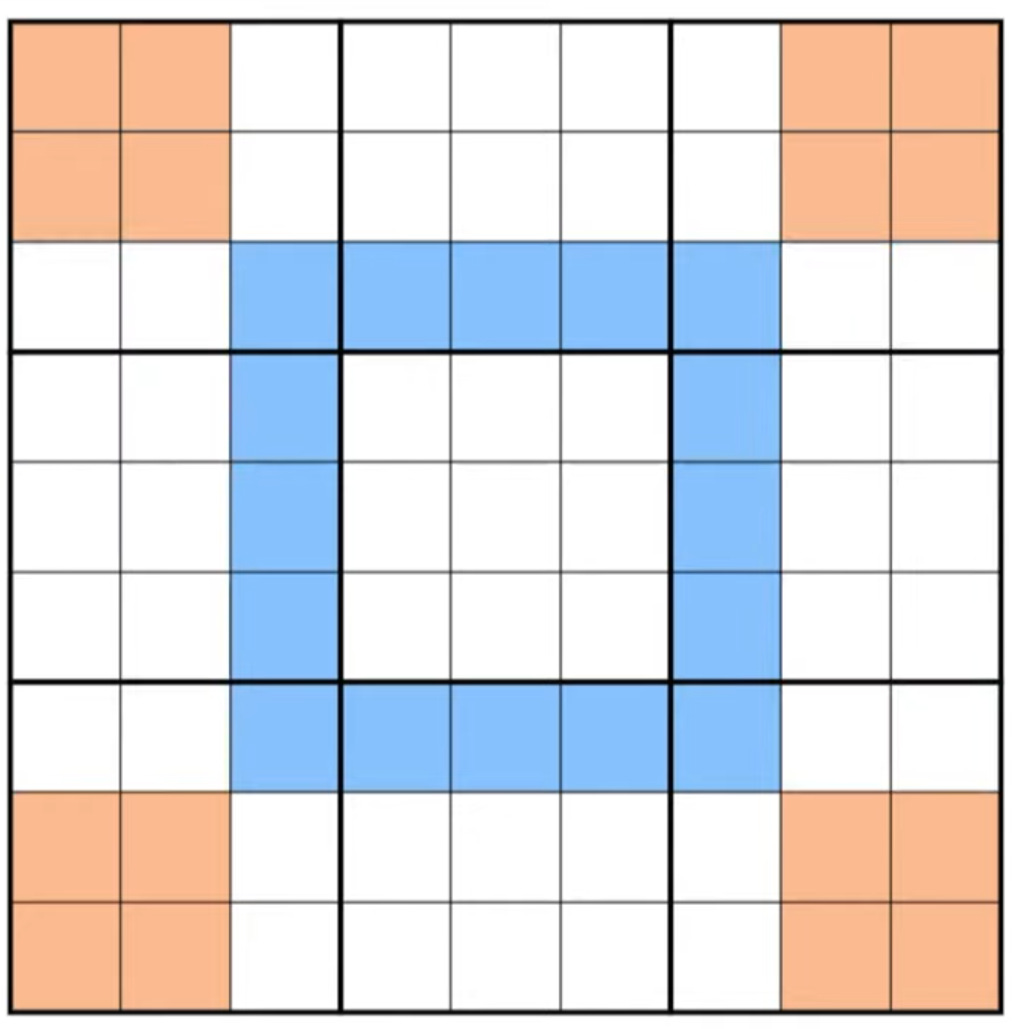
Here’s another way you could partition the sudoku: one blue ring in the center, and four orange anchors in the corners.

Is this any better than our frog and ostrich? Does it let us make any statements that we couldn’t easily make with row, column, and box? As it happens, yes. You can truthfully make the following statement: “The digits in the ring are exactly the same as the digits in the four anchors.”

Wait, what?

This surprising fact is called “Phistomofel’s Theorem”, named for the setter who initially popularized it. It’s a specific example of set equivalence theory that helped many people (myself included) understand it. Imagine that the letters 1 to 9 were all on tiles, like in a game of Scrabble. Each row, column, or box has the tiles 1 to 9 once each. Suppose you took the tiles in these two rows and these two boxes and put them in a blue sack:

Row 4, Row 7, Box 4, and Box 6 (image mislabeled) each have a run of the digits 1-9, so in total the blue sack has 36 tiles, four copies of each digit. Now, take a clone of your puzzle. This time, put these four columns in an orange sack:

Since both sacks have 4 runs of the digits 1 to 9, they have the same composition of digits inside them. But now, let’s superimpose the contents of the two sacks on to one grid, and look at the cells with both colors:

The cells with both colors are in both sacks. If you take the exact same cell out of both sacks, then clearly the two identical sacks will remain identical – you took the same thing out of each of them. You can do this for every cell with two colors. So, removing them all from our superimposed grid, we’re left with this:

That’s how we know that the digit composition of these regions – the ring and the anchors - are identical. And that means that this is a useful upgrade to our ontology, because now we can make statements like “There are two sixes in the ring, and only two spots in the anchors where a six can go, so there must be a six in each of them.” Those statements would be extremely tedious and unintuitive to make solely in terms of rows, columns, and boxes.

Once you’ve gotten the hang of Phistomofel’s Theorem, it’s a relatively short jump to using set equivalence theory in general. When we were picking runs of the digits 1-9, we made those particular choices because they happened to have a lot of overlap to them. But the core logic works for any regions that you make out of complete sets of the digits 1 to 9 – you can always eliminate the overlap and say that what’s left of the two regions are equal.

On its own, this is a neat bit of Sudoku trivia that might happen to pop up now and then in a puzzle. But what’s really interesting is when a puzzle is designed around this phenomenon. Setters (the term of art for people who design hand-crafted Sudoku puzzles for solvers to work through) can make a puzzle that’s virtually impossible using just rows, columns, and boxes, and can only be solved by upgrading your ontology. The Youtube channel Cracking the Cryptic has been an excellent source documenting this evolution.

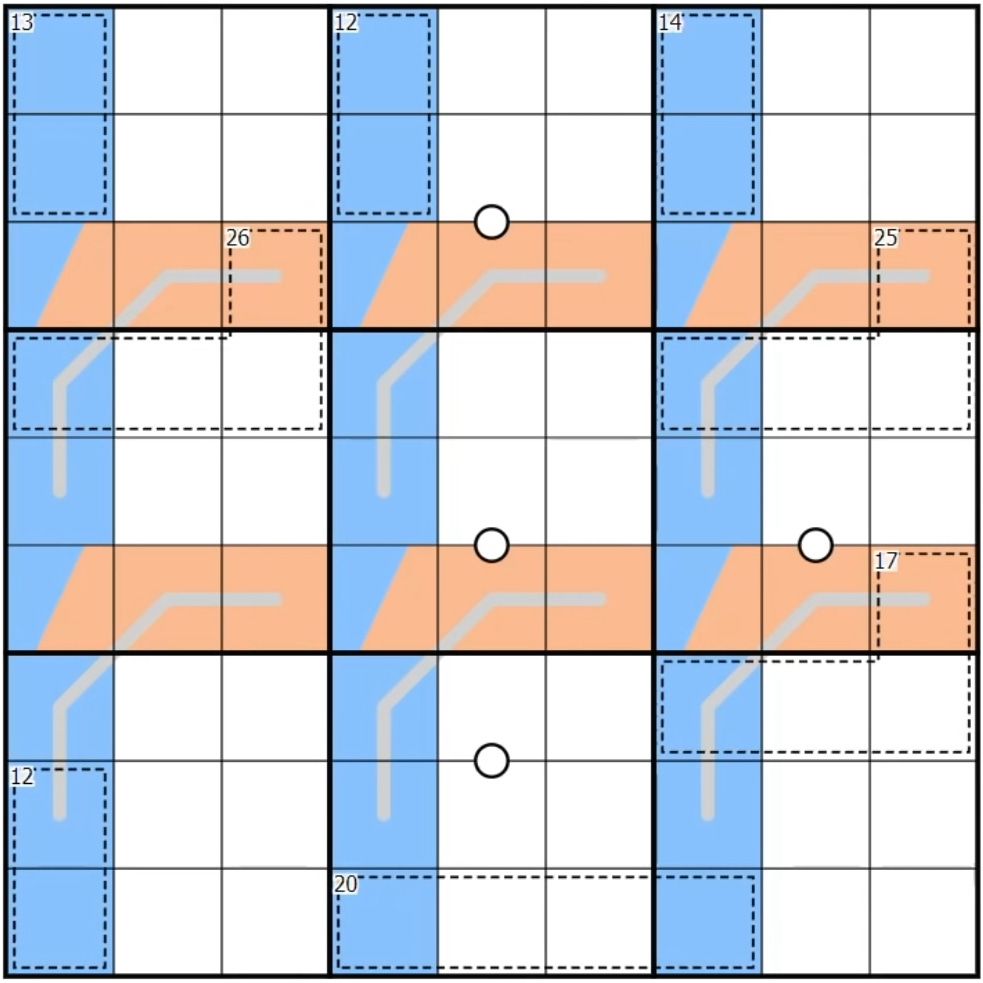
Now I can reveal where that quote up top came from: a video from Cracking the Cryptic called How to Make an Impossible Sudoku Easy. (I’ll be spoiling the break-in to the puzzle, so if you’re interested in trying it on your own first, do it now before reading on or watching the video.) Technically speaking, this isn’t quite a normal Sudoku, but a variant with some special rules:

The variant itself adds some words to our ontology. “This two-cell cage sums to 12, so it can’t have a 1 or a 2 in it.” “This line has a 5 on one end, so it must have a 5 on the other end.” “This digit is a 6, so the one on the other side of the dot is a 5 or a 7.” But such straightforward interpretations of the variant rules aren’t what interest us here. If Simon had seen these rules two years ago, he wouldn’t have struggled to notice what they mean. Set equivalence theory is special in that it’s not a straightforward application of set rules. It’s a new way of seeing, one that you need to know to invoke instead of seeing an obvious hint for.

In this case, what’s interesting is the interaction of set equivalence theory with the palindromic lines. Start with a column set that includes parts of all 6 lines: columns 1, 4, and 7.

Next, get a row set that includes parts of all 6 lines - rows 3 and 6:

This is a little different from how we did Phistomofel’s Theorem. The orange and blue sets aren’t equal exactly – we needed three lots of 1 to 9 for blue, while two were enough for orange. Instead, the claim here is that we know how much greater blue is than orange – specifically, it has exactly one more run of 1 to 9 than orange.

We start by removing overlapping cells:

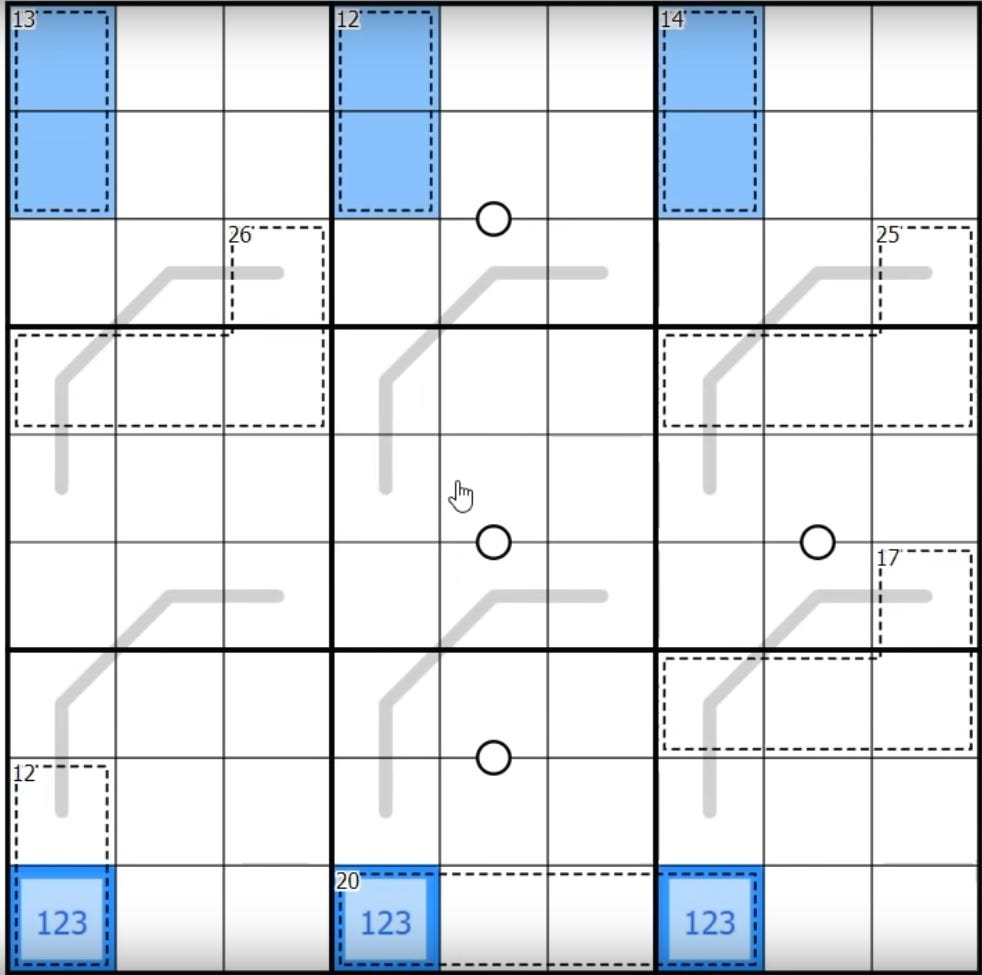
But we can go much further than that. Since we made sure to include the palindromic lines, we know that the blue segments of each line cancel out with the orange segments of the line. This leaves us with no orange digits at all, and 9 blue ones:

This means we know the composition of the blue digits. They’re exactly one set of the digits 1 to 9. The sum of the digits 1 to 9 is 45¹, and the top three cages sum to 13, 12, and 14. Since 13 + 12 + 14 = 39, the remaining digits must sum to 6. We know our only options are the digits 1 to 9 once each, which means that there’s only one way to do it – putting 1, 2, and 3 in the bottom three cells, in some order.

After finding this break-in, Simon remarked:

It’s not tricky – well, actually, I’m going to qualify that, because that’s a silly thing for me to have said. It’s absolutely impossible if you’ve not seen it before. Well, not impossible – virtually impossible. Certainly, probably impossible to do it at speed. But if you’ve seen it a few times before, it’s second-nature.

This is the hallmark of problems solved by ontological remodeling. You don’t want to say they’re tricky, exactly, because the new framework makes them feel pretty approachable. But without the new framework, they’re basically impossible. Trying to describe the difficulty of these problems is something of a trap, because so much of the difficulty depends on the description. Instead, you need to play around with new forms of expression and see which patterns are easy to describe with those forms.

The sheer simplicity of Sudoku makes it an excellent example for how powerful ontological remodeling can be even when it seems obvious which form to represent things in. Even if your generating rules are all related to rows, columns, and boxes, they can interact in such a way that you need new language to describe the interaction. In fact, this has become something of a sport on the channel, with puzzles like this one that start by showing a computer solver unable to solve a classic Sudoku logically (only getting the solution through brute forcing all possibilities), then setting a human loose on the puzzle to discover the hidden trick.

That’s as pure and straightforward a demonstration of ontological remodeling as you’re ever likely to get. Sudoku is a game whose rules only invoke rows, columns and boxes, but a computerized solver can’t describe the solve path with rows, columns, and boxes. The interplay of those rules leads to higher order patterns, and those higher order patterns need higher order language. But precisely because this example is so straightforward, it can give us a deceptive idea of how easy it is to notice that your ontology is lacking. While the solvers are in an ostensible “conflict” with the setters, it’s a thin bit of fun narrative over what is fundamentally a collaborative process. The setter wants people to notice the clever logical leap they demanded of their solvers, and that means they need people to solve it. Getting the warning that the computer can’t solve it gives you the enormous clue that you’ve got to try something new. You may not know what immediately, but you’re looking for the right sort of thing.

In fact, while there are plenty of puzzles that are totally incomprehensible without set equivalence theory, Phistomofel’s theorem itself has more tentative origins. Phistomofel created a puzzle that was best solved using the ring, but only published it when he was sure it could be solved “normally”. The ring was not a finding that solvers worldwide spontaneously developed when faced with a single, staggeringly beautiful puzzle. Instead, the origin story is far more pedestrian: Phistomofel talked about the ring in a forum post. Discussion followed that took the specific ring and anchors and generalized them into more generic statements about 1-9 sets. Only after the concept had reached a critical mass of socialization were most authors comfortable making puzzles where set equivalence theory was truly required.

So as great as puzzles are for practicing these techniques, you should never mistake a setters kindness for the indifferent illegibility of real-world problems. There are uncountably many things we’re thinking about the wrong way, but nature has no Phistomofel on deck nervously ensuring that it’s at least kind of possible to do it through brute force or starting a discussion with a helpful example. All we get are a bunch of problems that seem impossibly hard. Nothing about the world gives us an easy rule for which things are actually irreducibly tricky and which things just need better forms of description. That’s why it’s so important to cultivate an intuitive appreciation for the power of ontological remodeling. The reason this technique is so under-discussed and under-used is precisely because there’s no well-defined way to tell that it’s needed for a given problem. Individuals just have to take that leap of faith themselves, come up with a new way of seeing, and then demonstrate that problems that were once intractable are suddenly workable. We call those people “visionaries”, and we sure could use some more of them these days.

Thanks to Simon, Philip Newman, and Sam Cappleman-Lynes for reviewing a draft of this article.

1. This is a secret that Simon only tells his closest friends.