Desystemize #4

What is meta-rationality?

This is an article I’m both excited and nervous to write. Excited because this one is purely constructive and positive, not a cautionary tale of anything going wrong. In fact, it’s the introduction to a body of work by someone who is worried about the same Great Big Thing that we are. But this also means that my analysis will necessarily be more tentative and circumspect. Part of the power of the desystemic lens is that it’s so under-used and under-articulated that you can walk into just about any field and stumble upon useful insight by simply asking some basic questions about system correspondence and detail. When the field is deciding when to apply the desystemic lens, though, you don’t have the same low-hanging fruit to pluck. Alas.

So what is this field? Meta-rationality, a term of art that as far as I can tell was coined by David Chapman. I’ve been following his writing for years - if you know to look for it, the influence of the parable of the pebbles is clearly evident in the very first article of Desystemize about counting ticks. Somehow, though,  I managed to miss his primer "A first lesson in meta-rationality" until now. I can’t possibly explain all of meta-rationality in this newsletter. Chapman is working on a book called In the Cells of the Eggplant to do it, and it remains only partially finished after several years, so this single newsletter doesn’t have much hope. However, we can use the metaphors deployed in his first lesson to at least vaguely sketch what meta-rationality is and properly place it in the landscape of ideas relative to desystemization. (As someone who went ahead and also invented a word to describe this stuff instead of just using his, I feel a certain compulsion to defend myself!)

It’s my usual custom to link a post and say “the whole thing is worth reading”, but then give a summary for those who just want the highlights. Seriously, though - the whole thing is worth reading. This lesson uses puzzles as a tool to elicit understanding, and the frisson of attempting to solve them before reading the answer is a huge help in explaining the why. I will necessarily have to spoil the answers to those puzzles to use them as examples myself, so you won’t be able to come at it with the same fresh eyes if you read me first. Take the time, go read "A first lesson in meta-rationality", and come back here when you get a chance, okay?

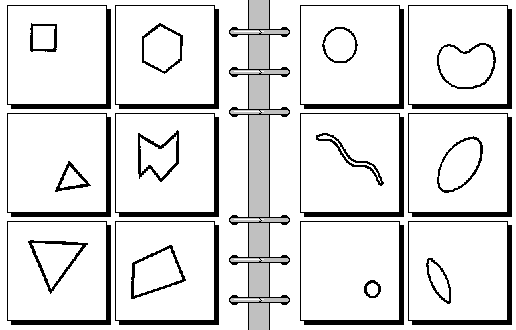
Okay. Well, I’m sure a few of you didn’t listen, so: this is what’s called a “Bongard problem.” Your goal is to figure out how the six images on the left are different from the six images on the right:

This is an easy one: straight lines on the left, smooth curves on the right. “Straight line” is something with a straightforward definition, and you can imagine applying a straight line detector to each of the twelve images in turn. You hear a beep on the left six and no beep for the right six, and go to bed secure in your powers of rationality. What makes Bongard problems interesting is that there’s no particular requirement that the criteria is that straightforward. Here’s a more fun one:

You know the answer straight away - triangles on the left, circles on the right. But what would happen if you applied a circle detector to the two on the left that are made of circles? If your circle detector beeps, you lose. And your circle detector DOES need to beep for the one on the right that’s made out of straight lines - how on earth are you going to pull that off? Not to mention that you have exactly the same problem with your triangle detector.

If your circle detector and triangle detector don’t work, how did you figure out the answer so fast? The trick is that there’s no such thing as a singular “circle detector”. That triangle made of circles really should make a circle detector beep in some contexts. If you’re detecting circles to figure out whether it will roll down the stairs if you drop it, it does you no good to confidently yell “triangle!” before sending a small avalanche of circles down to trip whoever has the misfortune of being below you while you attempt to achieve perfect rationality. “Circle” and “triangle” are not inherent properties of any of these twelve images. Instead, the images are laced with details that sometimes should be systemized into data like “circle” and “triangle” and sometimes should be ignored. The thing that makes a Bongard problem a problem is trying to figure out, for this given set of 12 images, which bits are extraneous in this particular case and which ones are not.

This is an incredibly important point, so it’s worth repeating. To solve a Bongard problem, you must engage in systemization. Abstract details need to be turned into data, so that you can make sure the data says one thing on the left side and one thing on the right side. This is not some meditation on how systemization is inherently wrong. But which details can be turned into data, and what that data should be, is a property of the problem, not the image. There’s no such thing as “truth” about these images that’s separate from the question we’re asking of them. Meaning is a byproduct of interaction, not an intrinsic property of anything.

Keeping this idea in mind, we’ll move on to a set of three problems meant to be solved in sequence. Number one:

Answer: three lines vs. five.

Number two:

Answer: three lines coming off a central point, vs. five lines coming off a central point.

Number three:

The big reveal: the rule of the last one is “four line segments vs five”, even though two of the entries on the right appear to have three line segments. But that’s only three line segments by the definition of “line segment” we used for the first two problems. Problem three is using “line segment” for anything coming off of a juncture point. The meaning of “line segment” depends on the company you keep.

This is in contrast to the high school “science is real” view of rationality as a constantly accumulating store of facts, as though there was a single body of knowledge of true statements. At first blush it seems that all we need to do is bail out the boat a bit more. Let’s just define “Line Type 1” as a continuous squiggly bit and “Line Type 2” as anything coming off of a junction, problem solved. Hey, we’re not rejecting the view of science as a body of work, we just doubled how much stuff is in it! We can define the Line Type 1s and Line Type 2s for any image we see. And if the good ship Rationality springs a leak every time a new Bongard problem shows itself -- why, caulking up the leaks is just the job of scientists, and won’t we have a better ship when all’s said and done?

Resist this impulse and sit with the word “line” a while. Whether you had seen the first problem before or after the third problem would have determined whether your initial idea of line was Line Type 1 or Line Type 2. And fixing your ignorance requires going back to the well of detail - the images themselves, not your abstractions of them as represented by line count. Whichever idea of “line” you came up with first wasn’t necessarily wrong when you came up with it, but it wasn’t precise enough to handle every question you could throw at it. This is happening everywhere, all of the time. We must systemize the nebulous world to get anything done, but systems annihilate detail, and there are uncountably many pairs of things that are “the same” in our representations of them but are actually different in some way we don’t know about yet and can only figure out by investigating the things themselves, not the representations.

This is the Great Big Thing that Desystemize and In the Cells of the Eggplant are both reactions to. You can be rational on a system, but there’s simply no such thing as global rationality, because processes that turn detail into data are always contingent on what ongoing work the processes are meant to support. But we need to systemize things to interact with a world beyond our immediate personal senses! This is Chapman’s focus, well-articulated in “A bridge to meta-rationality vs. civilizational collapse”. Rationality is a useful and necessary tool, but if we aren’t able to articulate its limitations and all of the circumrational work we unconsciously do to patch it up, then rationality’s failures will be co-opted as evidence by anti-rationalists to justify destroying systems we desperately need. 

Well, we just said that we like Chapman, but destroying systems is our whole shtick. How does this stuff fit together? If we think of meta-rationality as being more deliberate about the interface between world and data, then desystemization can rightly be viewed as a subtask of meta-rationality. To solve that last Bongard problem you must desystemize your old idea of “line”, re-observe the detailed world, and come up with a new systemization more appropriate to your current problem. On the level where you’re solving the problem, one step away from the real world, desystemization and resystemization come together in a beautiful and necessary dance of meta-rationality.

But the more steps away from the world you get - the more that your analysis is data about data about data - the more out of balance the whole enterprise of analysis becomes. This is the secret ingredient of the desystemic lens: it becomes more powerful with abstraction. When you diagnose the problem from on high, like Dr. Shrager did in Desystemize #2, you don’t have any tools to improve the correspondence to the real world - only to show that it’s broken. This is because our appetite for metrics has grown so much bigger than our ability to make them meaningful, with disastrous consequences for basically everyone. Chapman’s work is on how we can actually go about feeding ourselves more; we have the much easier and more entertaining remit of pointing and saying “Dude, that is pretty obviously going to make you sick.”

I find the parts of In the Cells of the Eggplant that we have so far endlessly fascinating; hopefully you will as well. It’s good to have a grounded understanding in what makes rationality work. If we’re going to survive as a species, then in my lifetime we’ll probably need to have better formal theories on this stuff. And I’m going to try my best to understand and incorporate that perspective, on the grounds that it is better to have enlightenment and not need it than need it and not have it. Luckily for the purpose of Desystemize, we don’t need to wait on that work to perform basic correspondence tests on our systems to the detailed world they claim to represent and marvel at the difference. Applying the desystemic lens is a subset of meta-rationality, but not one that’s relying on any completed theory to get the job done. A tagline for Desystemize could easily be: “Meta-rationality, but only the easy parts.” When numbers have gotten as far away from the world as many of the ones we see today, just having the sense to stop and look can be enough.

Speaking of looking at the world...let’s try to find a more concrete case study for next week, eh? Leave a comment if you have something worth looking at and subscribe if you want an email about it later.